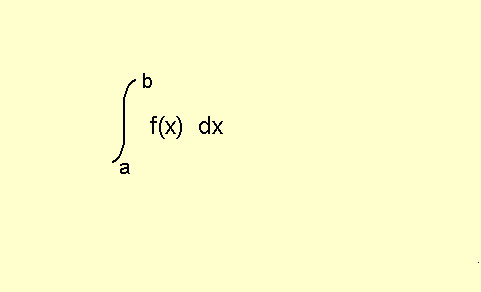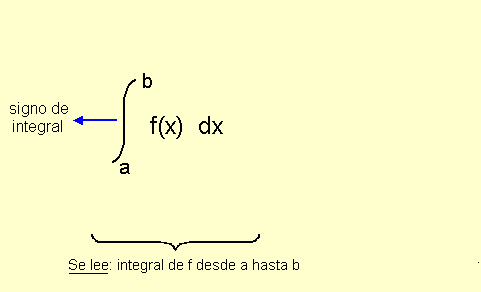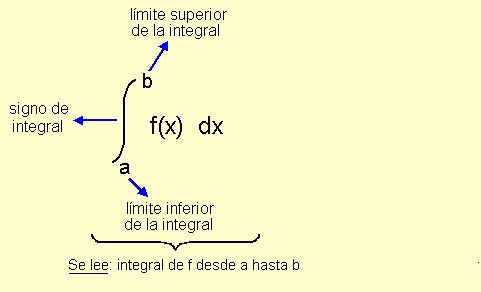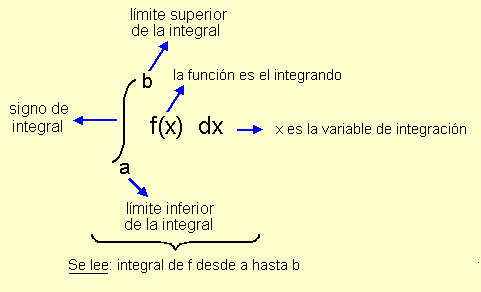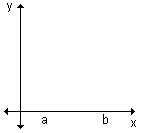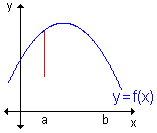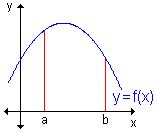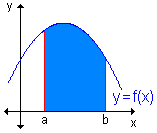Mostrando entradas con la etiqueta ANÁLISIS. Mostrar todas las entradas
Mostrando entradas con la etiqueta ANÁLISIS. Mostrar todas las entradas
UNIDAD 13: LA INTEGRAL DEFINIDA. CÁLCULO DE ÁREAS
Los contenidos que vamos a trabajar son:
- Integral definida. Área bajo una curva.
- Propiedades de la integral definida.
- Teorema fundamental del cálculo integral.
- Regla de Barrow.
- Cálculo de áreas.
UNIDAD 12: CÁLCULO DE PRIMITIVAS
Los contenidos que trabajamos en esta unidad son los siguientes:
Actividad resuelta con 50 integrales inmediatasy funciones racionales.
UN_12_INT_INMED.pdf
UN_12_INT_PARTES.pdf
UN_12_INT_SUSTITUCION.pdf
- Primitiva de una función. Integral indefinida. Propiedades.
- Cálculo de integrales inmediatas.
- Integración de funciones racionales.
- Integración por partes.
- Integración por cambio de variable.
Actividad resuelta con 50 integrales inmediatasy funciones racionales.
Actividad resuelta de integración por partes.
Recuerda......
Actividad resuelta de integración por cambio de variable (método de sustitución).
UNIDAD 11: REPRESENTACIÓN DE FUNCIONES
En esta unidad se trabajará la representación de funciones.
Es sabido que antes de proceder a la representación de una función se realiza una serie de cálculos previos: dominio de la función, puntos de corte con los ejes, simetrías, periodicidad, asíntotas, intervalos de crecimiento y decrecimiento, extremos relativos, curvatura y puntos de inflexión. A continuación, con esta información se procede a esbozar la gráfica de la función.
Se representarán funciones:
- Polinómicas.
- Racionales, grado tres como máximo en el numerador y dos en el denominador.
- Irracionales sencillas, con índice de la raíz dos y de radicando polinómios de hasta grado dos.
- Exponenciales, con exponentes polinomios de hasta grado dos o racionales de grado uno como máximo en numerador y denominador.
- Logarítmicas, de polinomios de grado menor o igual que dos.
- Funciones trigonométricas, seno, coseno y tangente.
- Valores absolutos, parte entera, a trozos y combinaciones sencillas de las funciones anteriores.
UNIDAD 10: APLICACIONES DE LA DERIVADA
Los contenidos que vamos a trabajar en esta unidad son los siguientes:
- Cálculo de límites. Regla de L´Hopital.
- Crecimiento y decrecimiento de una función. Relación con el estudio del signo de la función derivada.
- Máximos y mínimos de una función. Condición necesaria de máximo o mínimo en funciones derivables.
- Punto de inflexión, curvatura de una función. Relación de la curvatura con el estudio del signo de la segunda derivada.
- Cálculo de los máximos y mínimos de una función. Regla de la segunda derivada.
- Optimización de una función.
- Cálculo de los máximos y mínimos de una función en un intervalo cerrado.
NUEVO: En este pdf está el contenido teórico-práctico que estamos trabajando estos días en clase.
UNIDAD 9: DERIVADAS . TÉCNICAS DE DERIVACIÓN
Los contenidos que se trabajarán en esta unidad son:
- Derivada de una función en un punto.
- Interpretación física y geométrica del concepto de derivada de una función en un punto.
- Derivadas laterales.
- Función derivada.
- Cálculo de derivadas. Derivada de la suma, del producto y el cociente de funciones. Reglas de derivación.
- Derivada de la función compuesta. Regla de la cadena.
- Derivadas sucesivas. Derivadas de orden superior.
Hoja de actividades.
DOS FUNCIONES A TROZOS: F. SIGNO Y F. PARTE ENTERA
La función signo [f (x) = sgn(x)] es una función matemática definida por trozos. Se define como:
Observa que la función presenta una D.N.E. en x=0 de salto finito.
La función parte entera [f (x) = E(x)] a cada número real hace corresponder el mayor número entero que es menor o igual que él. Su representación gráfica es:
La función presenta D.N.E. de salto finito para todos los valores enteros de la variable x.
La función parte entera [f (x) = E(x)] a cada número real hace corresponder el mayor número entero que es menor o igual que él. Su representación gráfica es:
La función presenta D.N.E. de salto finito para todos los valores enteros de la variable x.
FUNCIONES EXTRAÑAS
En este post vamos a ver tres funciones bastante curiosas al tener propiedades poco comunes.
Función de Dirichlet
UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD
Los contenidos que vamos a trabajar en esta unidad son:
- Límite de una función en el infinito.
- Límite de una función en un punto. Límites laterales.
- Propiedades de los límites.
- Resolver indeterminaciones del tipo
- Definición de continuidad en un punto. Continuidad lateral.
- Discontinuidad en un punto. Tipos de dicontinuidades.
- Continuidad en un intervalo abierto y cerrado.
Hoja de ejercicios de límites con soluciones.
